As in the one-dimensional case, the output of such 2D systems can be expressed as the convolution of the input image x(m,n) with the impulse response h(m,n) of the linear and shift invariant system,
![]()
Similarly, a 2D system is said to be a finite impulse response (FIR) system or an infinite impulse response(IIR) system if its impulse response has finite or infinite support. Instead of having a one-dimensional impulse response h(n) characrterizing the filter, we now have with a two-dimensional impulse responses h(m,n).
Low-pass (LPF) and high-pass filters (HPF) can also be designed for 2D signals just like in the 1D case. For example, we know that the 1-D FIR filter described by the impulse response h(n)=[1 1 1 1 1]/5 will take the 5 point average of its input (which low-pass filters the input). If we now contruct a two-dimensional version of this filter, it will lead to a two-dimensional low pass spatial filtering of the image. The 2-D spatial frequency response of such a LPF is shown in the next figure.
Filter Impulse Respone
Saptial Frequency Response
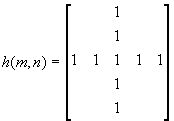
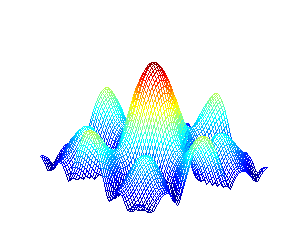
We can also obtain a more circular spatial frequency response
by using a modified version of the above low-pass filter with ones along
the main diagonal and the anti-diagonal as well.
Filter Impulse Response
Saptial Frequency Response


In this experiment, you will experience the effect of low pass and high pass
filtering on images. The filters that we use have been chosen so that their
spatial frequency response is as circular as possible. The
spatial frequency response of the filter you choose will always
be displayed before the original and the filtered images appear on the
screen.
![]() Important Note:
Usually, we associate the number p and 2p
in the discrete-time domain with the analog frequencies Fs/2
and Fs, respectively, where Fs is the sampling
frequency. In our case, in order to simplify the notation, the discrete-time
frequencies have been normalized to lie in the interval [0,1], with 1 corresponding
to the frequency Fs/2.
Important Note:
Usually, we associate the number p and 2p
in the discrete-time domain with the analog frequencies Fs/2
and Fs, respectively, where Fs is the sampling
frequency. In our case, in order to simplify the notation, the discrete-time
frequencies have been normalized to lie in the interval [0,1], with 1 corresponding
to the frequency Fs/2.