In this experiment you reconstruct a periodic continuous-time signal from its samples by using different basis functions. You can choose among rectangular pulses, triangular pulses, or truncated sinc pulses.

Assume a continuous-time signal is sampled at or above the Nyquist rate. Then it can be reconstructed from its samples according to the following reconstruction formula, which involves a sinc function,

where T denotes the sampling period (T=1/Fs, the inverse of the sampling frequency). We assume T is specified in
seconds and Fs in Hz.
 

From the above expression, we see that the perfect recovery of the continuous-time signal requires that we employ an infinite number of samples. More specifically, to recover the value of the signal at a time instant t, we center a sinc function at each sample and then add all such sinc functions. This perfect reconstruction procedure is of course not practical. For this reason, we shall use a truncated sum in our reconstruction procedure.

We shall also explore the use of basis functions other than the sinc, especially those that are easier to compute, such as the triangular or rectangular functions. The general reconstruction formula would then be
 

where p(t) denotes the pulse shape of our choice.. The above equation states that the output signal is produced by adding together many pulses, each centered at a particular sample, and also scaled by the amplitude of the sample x(n).

We consider three types of pulse waveforms in this experiment:
 

1. Rectangular pulse



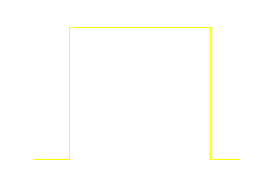
This is the simplest pulse shape. Its width is T and it corresponds to a zero-order hold operation. With this pulse waveform, we form a reconstructed signal that looks like a staircase waveform. We notice that in the reconstruction process, the pulses will not overlap and that the time-duration of each pulse is equal to the sampling period.

                         Pulse shape                                             Reconstruction
 
 
 
 

2. Triangular pulse



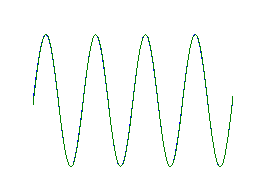
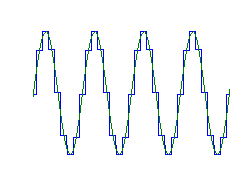
This corresponds to a first-order interpolation operation. In this case, the pulses will overlap (their width is 2T or twice the sampling period). Given this width, no more than two pulses will overlap. In other words, the resulting output of a  D/A converter at any given time will be the sum of  two scaled triangular overlapping pulses.

                          Pulse shape                        è                        Reconstruction
 
 

3. Truncated sinc pulse



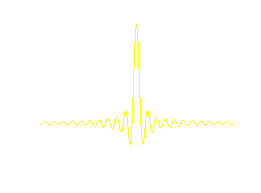
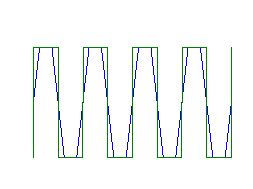
This is the truncated ideal interpolation waveform and corresponds to the truncation of the inverse Fourier transform of an ideal low pass filter with cutoff frequency at half the sampling rate. We notice that the time duration of this pulse is (2L+1)T. Consequently, at every sampling time we have (2L+1) pulses that overlap and the output of the D/A converter is then the  sum of (2L+1) scaled truncated sinc functions.

                        Pulse shape                                                    Reconstruction